고정 헤더 영역
상세 컨텐츠
본문

삼각형 내각의 합
삼각형 내각의 합은 다각형의 내각의 합을 구하는 바탕이 됩니다. 다각형을 몇 개의 삼각형으로 이루어 있는지 나눠보고, 삼각형 내각의 합을 바탕으로 계산하기 때문입니다.
삼각형 내각의 합이 180도임을 체험하는 방법으로 삼각형의 합동을 활용해보도록 하겠습니다.
우선, 다각형에서 다루게되는 몇가지 용어(변, 꼭짓점, 내각, 외각)를 확인하고 시작합니다.
다각형의 내각과 외각
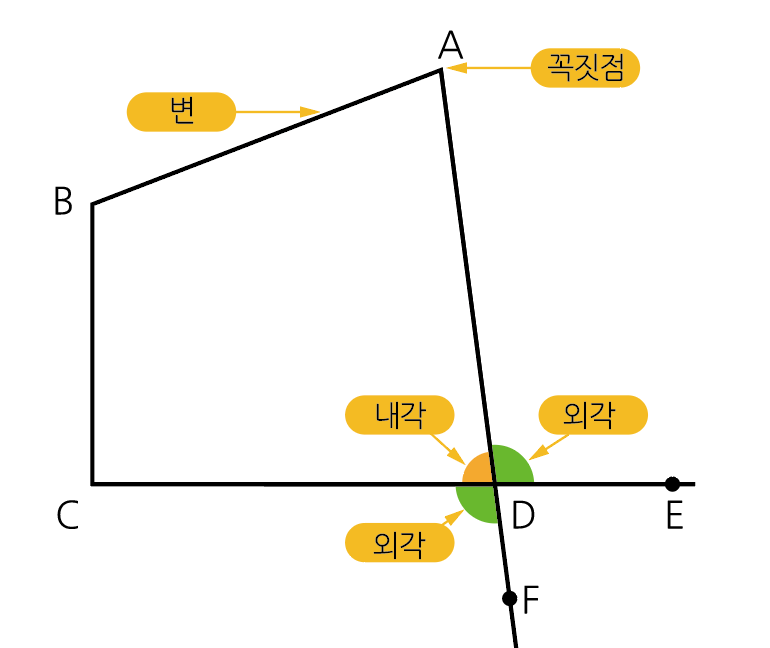
여러 개의 선분으로 둘러싸인 평면도형을 다각형이라고 부릅니다. 이때 선분의 갯수에 따라 3개는 삼각형, 4개는 사각형, N개인 다각형을 N각형이라 합니다. 이때 각 선분을 다각형의 변, 변과 변이 만나는 점을 다각형의 꼭짓점이라고 정의합니다.
다각형의 이웃하는 두 변으로 이루어진 각 중에서 안쪽에 있는 각을 다각형의 내각, 또 다각형의 각 꼭짓점에 이웃하는 두 변 중에서 한변과 다른 한 변의 연장선이 이루는 각을 그 내각에 대한 외각이라고 합니다. 예를 들어 다음 사각형의 변 CD, AD의 연장선 위에 각각 점 E, F를 잡을 때, ∠D는 내각이고 ∠CDF와 ∠EDA는 ∠D의 외각이 됩니다.
삼각형의 합동(대칭)으로 알아보는 삼각형 내각의 합
임의의 삼각형을 그려줍니다. 삼각형의 세 꼭짓점을 각각 A, B, C로 구분해줍니다.

선분 AB의 중점, 선분 AC의 중점을 이어 꼭지점 A가 밑면 BC와 닿게 접어줍니다. 새로 생긴 선분C'B'은 삼각형의 밑변 BC와 평행하고, 이때 생기는 삼각형 AC'B'와 삼각형 A'C'B'는 대칭입니다.

꼭지점 B가 점 A'에 닿도록 접고, 꼭지점 C도 점 A'에 닿도록 접어줍니다. 이때 삼각형 C'BD와 삼각형 C'DA', 그리고 삼각형 B'A'E와 삼각형 B'EC는 대칭입니다.
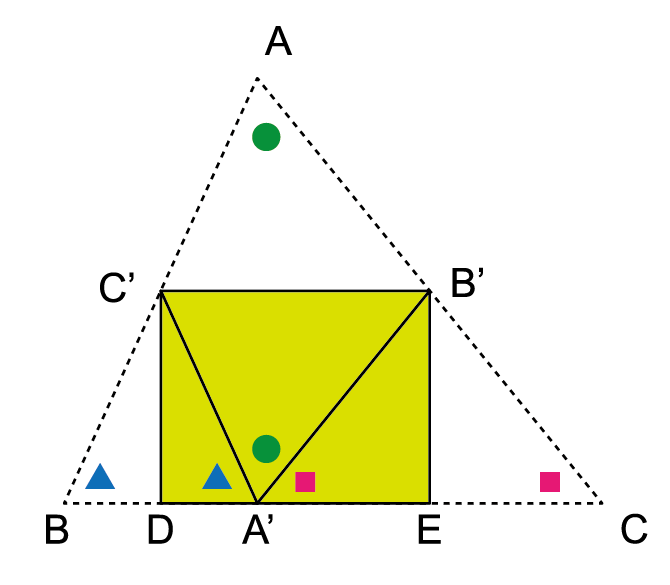
맨 처음 시작할때의 삼각형을 다시 떠올려봅시다. 처음 삼각형의 꼭짓점 A, B, C 세 각(아래 왼쪽 그림)이 다 접어진 후에는 점 A' 지점(아래 오른쪽 그림)에 다 모여있습니다. 세 각의 합이 수평으로 180도를 만들고 있는 것을 확인할 수 있습니다.

그리는 대신, 접어서 확인해도 좋아요
가지고 있는 종이를 삼각형 모양으로 자른 후, 접으면서 확인해보는 것도 좋습니다.
단 밑변과 평행하게 접는 것이 어려울 수 있는데, (위 도형 그림에서와 같이 A, B, C를 표시했다고 생각하고) 미리 선분 AB, 선분 AC를 반으로 살짝 접어 중점을 표시해둔 후 접는 것을 추천합니다.

'아이랑 노는척 공부' 카테고리의 다른 글
| [수학] 원뿔의 겉넓이를 계산하고 싶어요. 연습문제도 풀어봐요~ (0) | 2023.02.21 |
|---|---|
| [수학] 밑면 반지름 r일 경우, 원뿔 전개도 그리기, 원뿔 높이 구하기 (0) | 2023.02.20 |
| [수학] 합동을 이용한 도형의 분할 : 스핑크스 퍼즐(스핑크스 도형 PDF 첨부) (0) | 2023.01.20 |
| 자와 콤파스로 삼각기둥 전개도 직접 그려서 접어보기 (0) | 2023.01.13 |
| 삼각기둥 전개도가 궁금해? 여러가지 삼각기둥 전개도 알아보기 (0) | 2023.01.13 |




