고정 헤더 영역
상세 컨텐츠
본문
원뿔의 겉넓이를 이해하기 위해서는 전개도를 먼저 살펴봐야합니다.
삼각뿔은 3개의 옆면, 사각뿔은 4개의 옆면 등과 같이 N각뿔은 N개의 옆면을 가지고 있습니다.
그렇지만, 원뿔은 다른 뿔과 달리 밑면과 부채꼴 2개의 도형으로 이루어져 있습니다.
달리 생각하면 원의 넓이 공식만 알고 있다면, 더 쉬울 수 있습니다.
원뿔의 겉넓이
원뿔의 전개도의 예시입니다. 다른 다면체의 전개도보다 그리기 어렵게 느껴지는 것은 아래 전개도에서 보여지는 빨간색 호의 길이와 초록색 원주 길이를 같게 그려야하기 때문입니다.

전개도를 그리기 위해, 계산해야하는 식은 이전 글에서 정리했었으니 참고하세요.
[수학] 밑면 반지름 r일 경우, 원뿔 전개도 그리기, 원뿔 높이 구하기
다른 다면체 전개도보다 원뿔의 전개도를 직접 그리는 것을 어려워하는 아이들이 많습니다. 직접 계산해야하는 부분이 있지만, 원을 공부했으면 도전해볼 수 있게 해주세요 원뿔의 전개도를 그
lucia.tistory.com
밑면은 원의 넓이를 구하는 공식을 바로 적용하면 되고, 부채꼴의 경우는 원의 넓이에서 시작하되, 전체 360도 중, 부채꼴의 중심각이 어느 정도의 비율을 차지하는 지를 곱해주면 됩니다.
식으로 정리하면 다음과 같습니다.

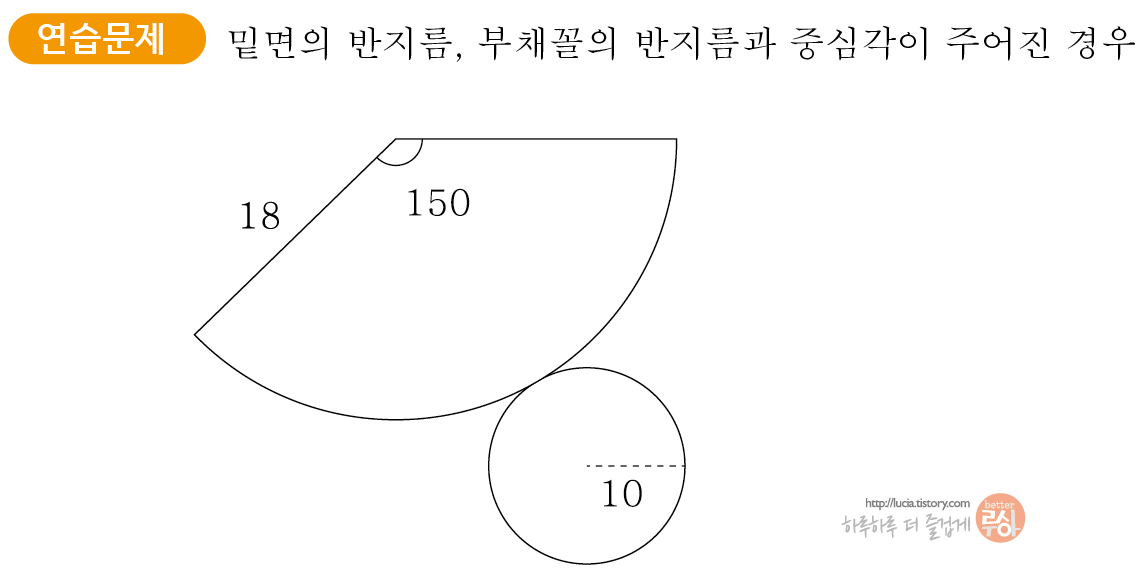
원뿔의 겉넓이를 계산할때 위의 예시처럼 전개도로 보여주면 바로 계산이 가능합니다.
밑면 원의 넓이, 부채꼴의 넓이를 각각 계산하여 합하면 됩니다.


원뿔의 밑면의 반지름과 원뿔의 높이를 알고 있다면, 부피는 아주 쉽게 구할 수 있습니다.
하지만, 겉넓이를 구하기 위해서는 전개도로 만들었을때 부채꼴의 반지름, 부채꼴의 중심각까지 구해야 합니다.
부채꼴의 반지름은 원뿔의 모선과 같으므로, 피타고라스의 정리를 활용합니다.
부채꼴의 중심각은 부채꼴의 호의 길이와 밑면 원주의 길이가 같아야함을 생각해보면 됩니다.

.
'아이랑 노는척 공부' 카테고리의 다른 글
| [수학] 원기둥은 각기둥과 다른가요? 전개도를 살펴보고 겉넓이과 부피 공식을 생각해봐요. (0) | 2023.03.21 |
|---|---|
| [수학] 원기둥과 원뿔의 부피 구하는 공식이 궁금해요 (0) | 2023.02.22 |
| [수학] 밑면 반지름 r일 경우, 원뿔 전개도 그리기, 원뿔 높이 구하기 (0) | 2023.02.20 |
| 삼각형 내각의 합은 180도, 접어보고 눈으로 확인! (0) | 2023.01.20 |
| [수학] 합동을 이용한 도형의 분할 : 스핑크스 퍼즐(스핑크스 도형 PDF 첨부) (0) | 2023.01.20 |




