고정 헤더 영역
상세 컨텐츠
본문
각기둥과 원기둥
각기둥은 위와 아래에 있는 면이 서로 평행이고 합동이며, 옆면이 사각형인 기둥 모양의 입체도형으로 바닥면의 모양을 기준으로 삼각기둥, 사각기둥 등, 바닥면의 모양이 N각형이라면, N각기둥으로 부릅니다.
이때 N의 값이 무한히 커지면 어떻게 될까요?
다음 예시처럼, 팔각형, 십각형, 십이각형 등 N값이 무한히 커질때 원의 모양이 되는 것으로 확장하여 생각해봅니다.

원기둥은 각기둥과 같이 위와 아래에 있는 면이 서로 평행이고, 이때 그 면이 합동인 원입니다. 한가지 더 주의할 것은 각기둥에서 옆면이 사각형 모양이라는 부분이 있었지만 원기둥은 잘게 쪼개진 무수히 많은 사각형모양이 모여 옆면을 만들고 있습니다. 그렇기 때문에, 다음 예시와 같이 위와 아래에 있는 면의 평행과 합동만으로는 원기둥이 아닌 입체도 생각할 수 있으니 주의해야합니다.

원기둥의 전개도
다른 각기둥의 전개도보다 원기둥의 전개도는 더 쉽습니다. 삼각기둥, 사각기둥, 오각기둥.. 다른 각기둥은 밑면의 모양이 정삼각형이냐, 직각삼각형이냐, 이등변삼각형이냐를 생각하면서, 각 변의 길이를 구해 옆면을 그리는 등 어려울 수도 있습니다. 하지만, 원기둥은 밑면이 원입니다. 원에서는 반지름의 길이만 생각하면 됩니다.
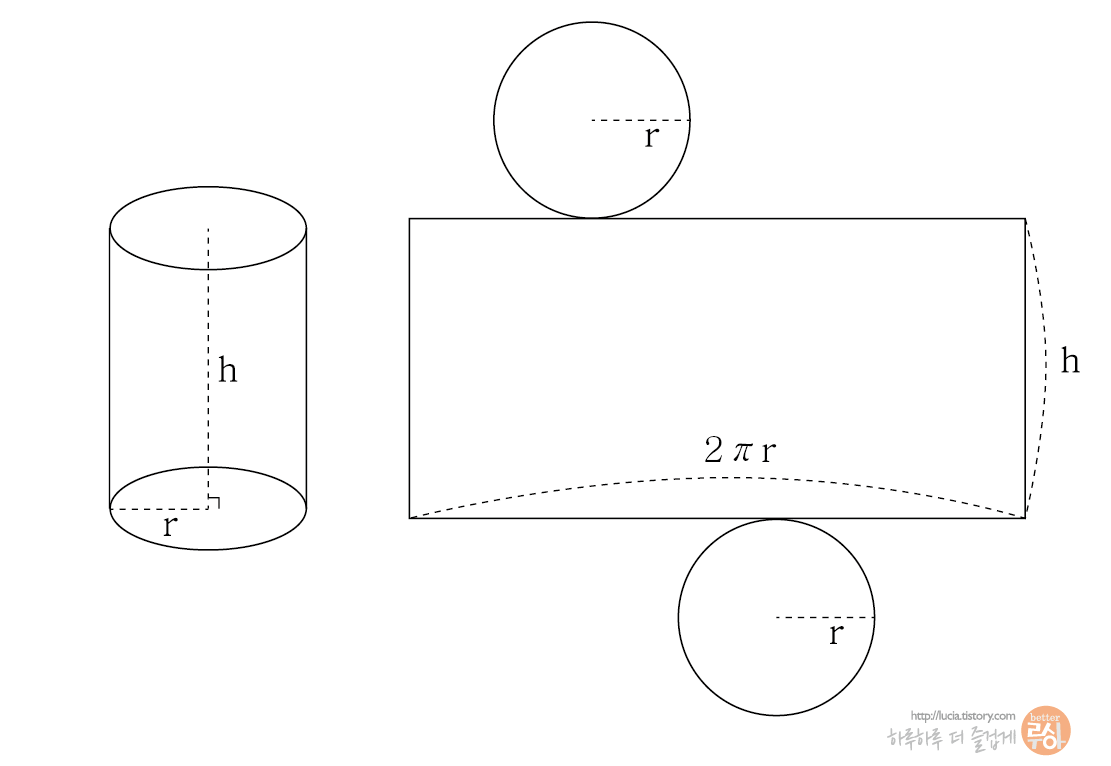
원기둥은 밑면 원의 반지름, 그리고 기둥의 높이값이 있는데, 이때 옆면을 만드는 직사각형의 가로길이는 밑면의 원주길이와 같아야 합니다.
잠시 다른 각기둥의 전개도를 살펴볼까요?
전에 밑면의 모양이 다양한 사각형의 전개도가 어떻게 달라지는지 알아보았던 게시글입니다. 이미 알고 있는 내용이라면 패스하시면 됩니다.
여러가지 모양의 사각기둥, 전개도는 어떻게 달라질까?
각기둥의 정의를 정확하게 알고 있다면, 약간의 변형이 가해진 경우에도 생 각하고 문제를 해결할 수 있는 힘이 생깁니다. 사각기둥의 경우에도 밑면(바닥면)의 모양에 따라 여러가지 모양이 나
lucia.tistory.com
원기둥의 부피와 겉넓이 구하는 공식
원기둥의 부피는 원모양을 차곡차곡 쌓아 높이만큼 만들어지는 것이므로 원의 넓이에 높이를 곱해주면 됩니다. 겉넓이는 전개도에서 본것처럼 원모양의 밑면 2개와 사각형으로 이루어져 있으므로, 밑면 원넓이에 2배를 하고 옆면 사각형의 넓이를 더해주면 됩니다. 옆면 사각형의 세로는 원기둥의 높이, 가로는 밑면 원의 한바퀴 둘레, 즉 원주입니다.

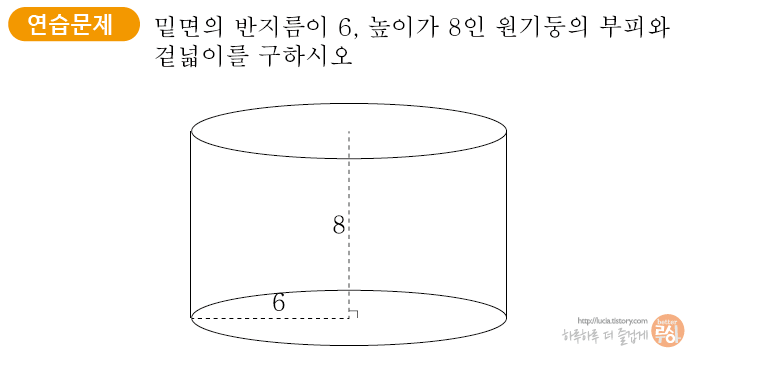
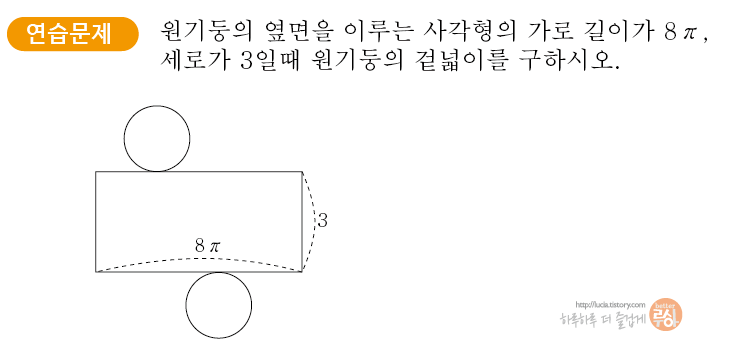
아래 연습문제를 2개 만들어봤습니다. 밑면과 높이 값이 주어진 경우에는 기본 공식을 생각하며 계산하면 됩니다. 두번째 연습문제처럼 밑면의 반지름 값을 주지 않았다면, 원주와 옆면 사각형의 가로길이가 같아야함을 생각하며 반지름을 먼저 구하고 진행하면 됩니다.


'아이랑 노는척 공부' 카테고리의 다른 글
| 알지오매스3D : 입체도형 그리기, 각기둥와 각뿔 (0) | 2023.04.13 |
|---|---|
| 알지오매스3D : 전개도 그리고 입체도형 접기(정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체) (0) | 2023.04.13 |
| [수학] 원기둥과 원뿔의 부피 구하는 공식이 궁금해요 (0) | 2023.02.22 |
| [수학] 원뿔의 겉넓이를 계산하고 싶어요. 연습문제도 풀어봐요~ (0) | 2023.02.21 |
| [수학] 밑면 반지름 r일 경우, 원뿔 전개도 그리기, 원뿔 높이 구하기 (0) | 2023.02.20 |




