고정 헤더 영역
상세 컨텐츠
본문
이제는 현찰 사용이 줄다보니, 동전 구경하기도 쉽지 않네요.
동그란 동전을 쌓아 보여주면 원기둥의 부피로 연결시켜 이해할 수 있겠다 싶어 동전을 모아봤습니다.

위치를 지정하는 점, 점이 이동한 자취를 선, 선이 확장되면 면이 되는 것처럼, 원을 겹겹히 쌓아 만들어지는 것이 원기둥입니다.

원을 겹겹히 쌓아 올리면 다 원기둥이 되는 것은 아닙니다.
아래의 예시는 원을 겹겹히 쌓아 올렸지만 원기둥이 아닙니다.
원기둥이 되려면 밑면과 위면, 그리고 그 사이의 세로축에 수직으로 자른 단면의 크기가 모두 같은 원이어야 합니다.
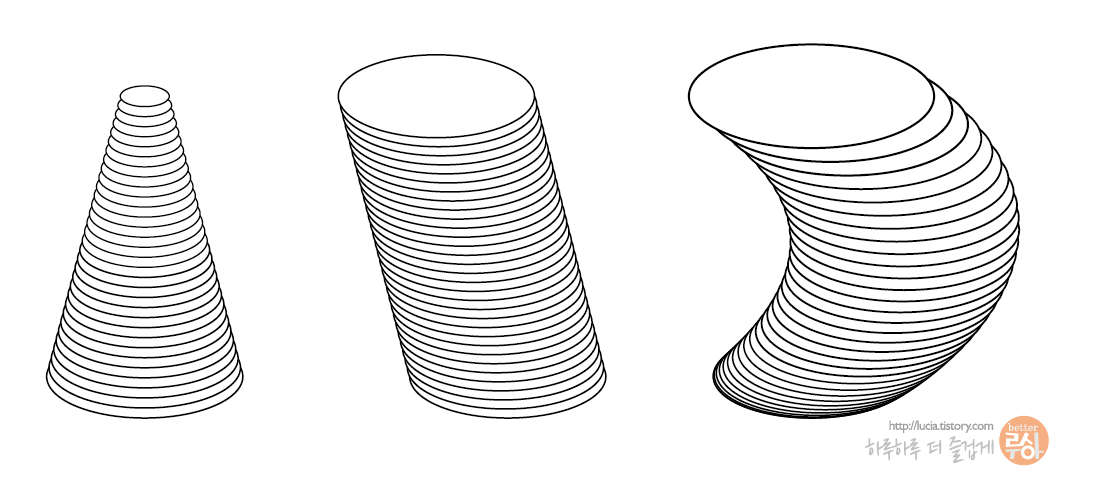
밑면과 위면, 세로축에 수직인 중간단계의 단면의 크기가 모두 같은 원기둥은 다음과 같은 형태를 가지고 있습니다.
밑면의 반지름을 r, 원기둥의 높이를 h라고 할때, 원기둥의 부피는 다음과 같이 계산됩니다.
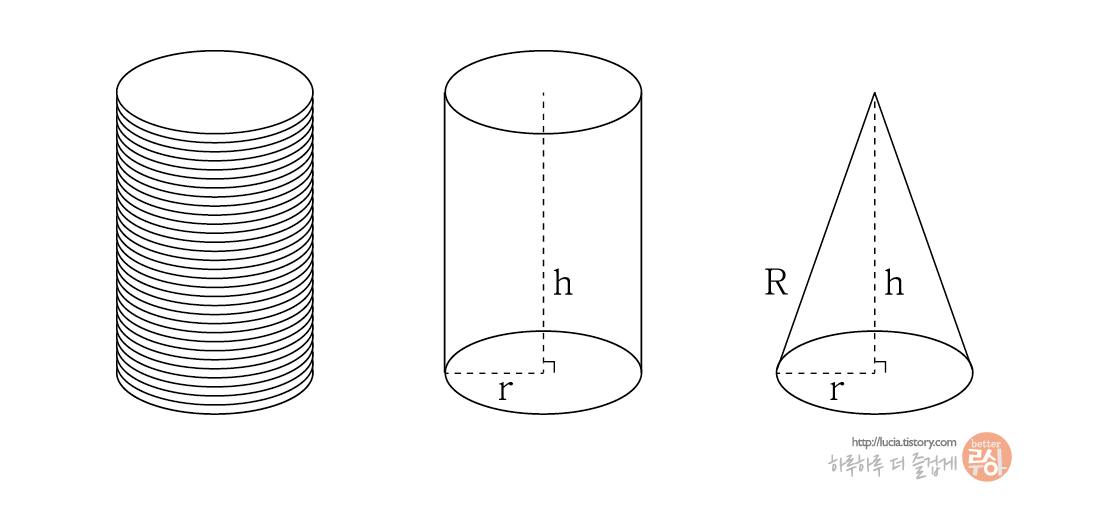
동전을 예로 들었지만, 두께가 0에 가까운 동전을 높이 h가 될때까지 쌓는다고 생각하면 이해하기 쉽습니다.
그래서 밑면의 넓이에 높이를 곱해주어 원기둥의 부피를 구할 수 있습니다.
기둥과 뿔의 부피관계는 기둥의 부피에 1/3을 곱하면 뿔의 부피가 됩니다.

이 공식을 활용하여 원뿔의 높이를 구하라는 문제도 해결할 수 있습니다.
원뿔의 부피를 계산하는 공식을 원뿔의 높이 h에 대하여 정리하면 다음과 같습니다.


원뿔의 높이를 구하는 공식을 따로 외우기 보다는 원기둥의 부피를 구하는 공식만 외우고, 원뿔의 부피는 원기둥 부피의 1/3이라는 점만 기억하는 것이 어떨까요?
그 후, 다음과 같이 알고 있는 값들을 대입시키고, 모르는 값에 대해 식을 정리하면 됩니다.
원뿔의 높이 구하는 공식, 원뿔의 반지름 구하는 공식 따로 외우려면 아이들이 너무 힘들어할 것 같습니다.
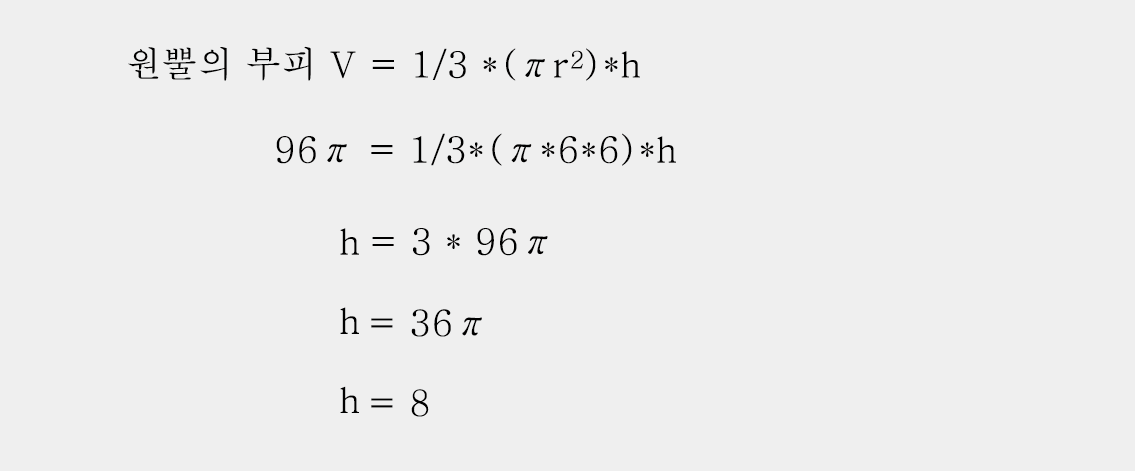
왜 뿔의 부피가 기둥 부피의 1/3이냐고 물어보는 아이에게....
원기둥과 원뿔의 부피관계 이해는 전개도를 접어보는 방식으로는 힘들고, 입체에 물을 채웠을때를 살펴보는 방식으로 설명하곤 합니다. 대신, 접어보기 수월한 사각기둥과 사각뿔을 사용하여 부피관계를 이해할 수 있습니다.
다음 전개도를 직접 접어볼 수 있는 아이는 체험하게 해주고, 어렵다면 지도하시는 분이 미리 접어둔 것을 맞춰보면서 공간을 이해할 수 있게 해주세요.
[추가] 사각뿔과 사각기둥 체험 전개도 PDF https://lucia.tistory.com/129
접어보자! 뿔의 부피는 기둥의 1/3이라는데. 진짜?
입체도형을 배우면서, 넓이를 구하는 가로, 세로에 높이의 개념이 추가됩니다. 그래도, 사각기둥, 삼각기둥, 원기둥은 쉽게 이해하는 편인데, 뿔의 부피를 구하기 위해서 기둥의 부피를 3으로 나
lucia.tistory.com
'아이랑 노는척 공부' 카테고리의 다른 글
| 알지오매스3D : 전개도 그리고 입체도형 접기(정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체) (0) | 2023.04.13 |
|---|---|
| [수학] 원기둥은 각기둥과 다른가요? 전개도를 살펴보고 겉넓이과 부피 공식을 생각해봐요. (0) | 2023.03.21 |
| [수학] 원뿔의 겉넓이를 계산하고 싶어요. 연습문제도 풀어봐요~ (0) | 2023.02.21 |
| [수학] 밑면 반지름 r일 경우, 원뿔 전개도 그리기, 원뿔 높이 구하기 (0) | 2023.02.20 |
| 삼각형 내각의 합은 180도, 접어보고 눈으로 확인! (0) | 2023.01.20 |




