고정 헤더 영역
상세 컨텐츠
본문
다각형의 내각과 외각
여러 개의 선분으로 둘러싸인 평면도형을 다각형이라고 부릅니다.
이때 선분의 갯수에 따라 3개는 삼각형, 4개는 사각형, N개인 다각형을 N각형이라 합니다. 이때 각 선분을 다각형의 변, 변과 변이 만나는 점을 다각형의 꼭짓점이라고 정의합니다.
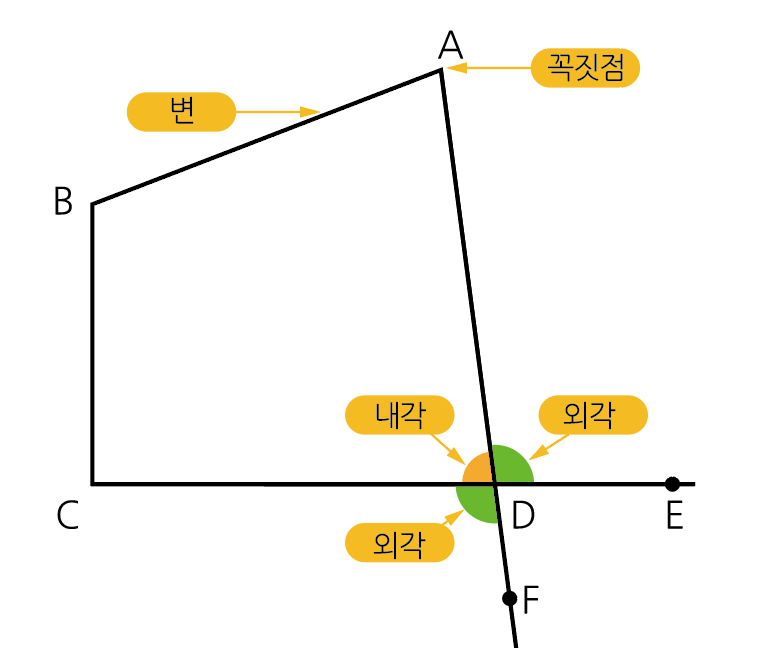
다각형의 이웃하는 두 변으로 이루어진 각 중에서 안쪽에 있는 각을 다각형의 내각, 또 다각형의 각 꼭짓점에 이웃하는 두 변 중에서 한변과 다른 한 변의 연장선이 이루는 각을 그 내각에 대한 외각이라고 합니다.
예를 들어 다음 사각형의 변 CD, AD의 연장선 위에 각각 점 E, F를 잡을 때, ∠D는 내각이고 ∠CDF와 ∠EDA는 ∠D의 외각이 됩니다.
삼각형의 내각과 외각에는 어떤 성질이 있을까?
다음은 A4 사이즈의 종이를 한장 준비합니다. 종이위에 여러개의 삼각형을 자유롭게 그리게 합니다.
꼭 아래와 같은 모양이 되지 않더라도, 다른 모양의 삼각형이 3개 정도 만들어지게 선을 그어주고, 잘라줍니다.


잘라진 삼각형 중, 다른 모양의 삼각형 3개를 고르게 하고, 각 꼭지점에 각각 다른 색의 스티커를 붙여줍니다.
스티커가 없을 경우, 색연필로 표시를 해둬도 됩니다. 이는 각을 잘랐을때 어떤 삼각형의 각이었는지 구분하기 위함입니다.
삼각형을 이루는 3개의 각을 이어 붙여보기 위해, 아래 사진에 초록색 선 표시와 같이 삼각형을 잘라줍니다.
- 초록스티커가 붙은 삼각형 >> 예각 삼각형
- 파랑 스티커가 붙은 삼각형 >> 둔각 삼각형
- 빨강 스티커가 붙은 삼각형 >> 직각 삼각형

다음 그림과 같이 삼각형의 3각들이 스티커 색 별로 모두 잘라졌습니다.
스티커가 붙은 각이 원래 삼각형에서 내각을 표시한 것이므로, 같은 색의 스티커 3개가 모아지도록 배치해 봅니다.

스티커 색 별로 모았더니, 3개의 내각을 합하면 모두 180도가 되는 것을 확인할 수 있습니다. 삼각형이라면, 모양이 다르더라도 3개의 내각의 합은 항상 180도가 된다는 것을 확인하게 해줍니다.
* 삼각형의 세 내각의 크기의 합은 180도이다.
*삼각형의 한 외각의 크기는 그와 이웃하지 않는 두 내각의 크기의 합과 같다.

다각형에서 내각의 크기의 합은 어떻게 구할까?
삼각형 내각의 크기의 합이 180도임을 활용하여, 다음 다각형을 삼각형으로 나눠서 생각해보게 합니다.
사각형의 경우 삼각형 2개로 나뉘므로 사각형 내각의 합은 180도X2=360도가 됩니다.
마찬가지로 육각형 내각의 크기 합은 180도X4=720도가 됩니다.

일반적으로 N각형의 한 꼭짓점에서 대각선을 모두 그으면 (N-2)개의 삼각형으로 나뉘어지므로 N각형에서 내각의 크기의 합은 180도X(N-2)이가 되는 것을 알 수 있습니다.

정다각형의 한 내각의 크기
정다각형에서 한 내각의 크기를 구할 수 있을까?
정다각형은 내각의 크기가 모두 같으므로 정다각형의 내각의 크기의 합을 안다면 한 내각의 크기를 알 수 있게 됩니다.
내각의 크기의 합을 똑같이 나누면 되므로, 내각의 크기의 합을 꼭짓점 갯수로 나눈 것과 같습니다.
위의 오각형을 예로 들면, 오각형의 내각의 크기 합은 180도 X 3 = 540도입니다. 정오각형이라면, 5개 내각의 크기가 모두 같으므로 정오각형의 한 내각의 크기는 540도를 5로 나눈 108도가 됩니다.
즉, 정N각형에서 한 내각의 크기는 다음과 같이 구할 수 있습니다.

잠깐, 아이가 이렇게 할 수도 있어요
다각형의 내각의 합을 구하기 위해, 다각형 내부를 삼각형으로 분할하여 계산하는 방법을 사용하는데, 우리 아이들은 다음과 같이 나눌지도 모릅니다.
오히려 이렇게 하면 왜 안되나요? 눈 동그랗게 뜨고 물어볼지도 모릅니다^^

저렇게 분할을 해도 되지만, 그림을 자세히 보시면, 5개로 분할한 경우 오각형 안쪽의 삼각형은 5개, 삼각형의 내각은 3개씩이니 총 15개의 각이 있지만, 오각형에 사용된 삼각형의 내각은 10개 뿐입니다.
5개는 오각형의 중심에 모아져있습니다. 그러니, 이런 경우 삼각형 1개의 내각 합인 180도에 5배를 해주고, 가운데에 모여있는 5개 각의 합인 360도를 뺄 수 있게 설명해주시면 됩니다.
즉, (180도 X 5) - 360도 = 540도로 같은 값이 나옵니다.
4개로 분할한 그림에서도 4개 삼각형의 내각 12개 중 9개만 오각형의 내각을 구성하고 가운데 3개는 오각형의 내각이 아닙니다. 그러므로 삼각형 1개의 내각 합인 180도에 4배를 해주고, 가운데에 모여있는 3개 각의 합인 180도를 뺄 수 있게 설명해주시면 됩니다. 즉, (180도 X 4) - 180도 = 540도로 역시 같은 값이 나옵니다.

[추가] 설명 및 활동과정 영상자료입니다. 필요하신 분 참고하세요^^ https://youtu.be/ClS5bomnDOk
[추가] 대각선 개수 문제 나오면 세는 사람. 꼭보세요. https://lucia.tistory.com/335
대각선 몇개냐구? 설마.. 세봤어? 대각선 개수 구하는 공식 쉽게 이해하기
초등 4학년 도형파트에 다각형의 대각선 개수 문제가 있습니다. 문제를 풀다가 막히면, 대각선 개수 구하는 공식을 찾는 아이들이 있는데 어떻게 공식이 만들어졌는지를 생각해보면, 공식을 외
lucia.tistory.com
[추가] 도형을 돌렸을때 어떤 입체가 될까요? https://lucia.tistory.com/125
[활동지 PDF포함] 회전체 알아보기 : 빙글 돌리면 어떤 입체가 만들어질까?
회전체 알아보기 회전체는 평면도형을 회전시켜 만든 입체도형을 말합니다. 정확하게는 평면도형을 한 직선을 축으로 하여 1회전 시킬 때 생기는 입체도형입니다. 원기둥은 직사각형의 한 변을
lucia.tistory.com
[추가] 내각에 대해 이해했다면, 다음은 외각의 합!! https://lucia.tistory.com/47
다각형 외각의 합, 체험으로 이해하기 2탄
다각형의 내각과 외각 여러 개의 선분으로 둘러싸인 평면도형을 다각형이라고 부릅니다. 이때 선분의 갯수에 따라 3개는 삼각형, 4개는 사각형, N개인 다각형을 N각형이라 합니다.
lucia.tistory.com
.
'아이랑 노는척 공부' 카테고리의 다른 글
| 밀도 차이로 움직이는 라바램프 (0) | 2021.06.11 |
|---|---|
| 칼레이도사이클 전개도와 접는법 (0) | 2021.06.09 |
| 색종이 1장으로 삼각뿔을 만들어봐요 (0) | 2021.06.04 |
| 엄마, 크게 접어주세요 : 정십이면체 편 (0) | 2021.06.03 |
| 양면접시 좋지? 삼면접시 접어볼래? (0) | 2021.05.27 |




