고정 헤더 영역
상세 컨텐츠
본문

초등 4학년 도형파트에
다각형의 대각선 개수 문제가 있습니다.
문제를 풀다가 막히면,
대각선 개수 구하는 공식을 찾는 아이들이 있는데
어떻게 공식이 만들어졌는지를 생각해보면,
공식을 외우지 않더라도 해결할 수 있습니다.
이해하고 문제를 풀다보니
저절로 외워진다면 더 좋지 않을까요?
사각형부터 생각해볼께요.
대각선은 한자 그대로 풀어 해석하면 그 뜻을 알 수 있습니다. 즉, 對 (대할 대), 角 (뿔 각), 線 (줄 선)으로 다각형에서 이웃하지 않은 두 꼭짓점을 이은 선분을 말합니다.
앞의 정의를 생각해보면 삼각형은 점이 3개라서, 한 점을 기준으로 하면 나머지 두 점은 모두 연결되어 있기 때문에 대각선을 그을 수가 없어요.
그래서 사각형부터 대각선을 만들 수 있습니다.
아래 그림에서처럼 한 꼭지점을 기준으로 보면, 다른 점이 3개가 있고, 2개의 점은 이웃하고 있으니, 나머지 1개의 점으로 이어지는 대각선을 그을 수 있습니다.
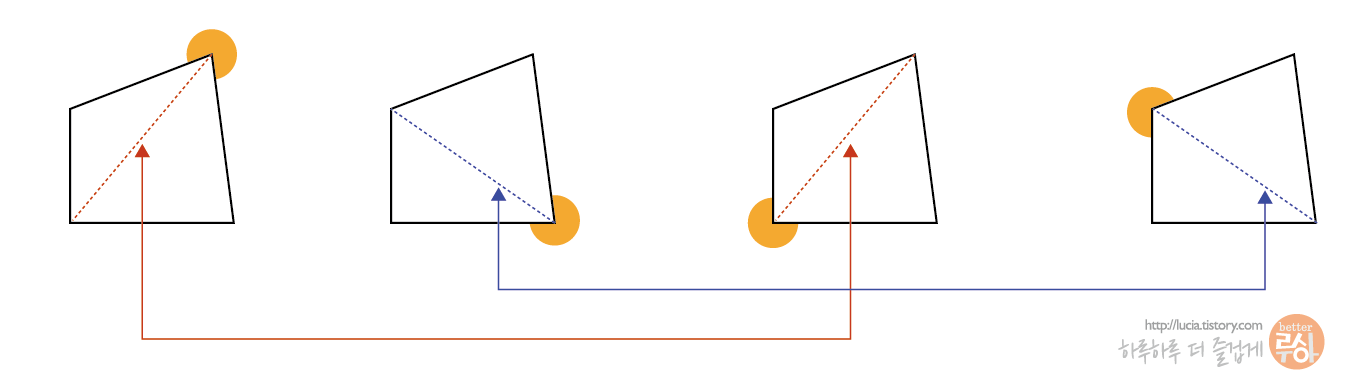
사각형에서는 한 꼭지점에서 1개의 대각선을 그을 수 있고, 전부 4개의 꼭지점이 있으니 각각의 꼭지점에서 1개의 대각선을 그을 수 있습니다.
그런데, 잘 살며보면 빨간 점선으로 표시한 대각선 2개, 그리고 파란 점선으로 표시한 대각선 2개는 같은 대각선입니다.
2개의 점을 이어 만들어지는 대각선이므로, 2개씩 중복하여 생깁니다.
오각형도 볼까요?
사각형에서 한단계 더 올려 오각형을 보겠습니다.
오각형은 꼭지점이 5개이므로, 1개의 꼭지점을 기준으로 보면 4개의 점이 있고, 2개의 점은 이웃하고 있으니, 나머지 2개의 점으로 대각선을 그을 수 있습니다.
한 꼭지점에서 2개의 대각선을 그을 수 있고, 꼭지점은 모두 5개가 있습니다.
앞의 사각형에서와 같이 대각선은 모두 2개씩 중복되어 만들어집니다.

N각형으로 확장해서 생각해봐요
(1) 1개의 꼭지점에서 그을 수 있는 대각선의 개수는 몇개일까?
N각형에서 1개의 꼭지점에서 그을 수 있는 대각선은 N개의 꼭지점에서 기준이되는 1개의 점, 그리고 그 점와 이웃하고 있는 2개의 점으로는 대각선을 그을 수 없으므로 N-3개가 됩니다.
(2) N-3개의 대각선을 만들 수 있는 꼭지점의 수
한개의 꼭지점마다 N-3개의 대각선을 만들 수 있고, N각형에는 N개의 꼭지점이 있으므로 (N-3)*N개를 그릴 수 있습니다. 그런데, 이 개수는 한개의 대각선에 대해서 2번씩 중복되어 나온 값입니다.
(3) 중복되어 계산된 값 정리
대각선은 양쪽 끝 두개의 점으로 만들어져 있어서, 모두 2번씩 세어졌으므로 2로 나눠줘야 합니다.

공식에 맞춰 다시 계산해볼까요?
사각형의 대각선 개수
N=4이므로,
(4-3) * 4 * 0.5 = 2
오각형의 대각선 개수
N=5이므로,
(5-3) * 5 * 0.5 = 5
이 정도까지는 그려서 세보면 되겠지요? 그럼 십이각형의 대각선 개수?
십이각형은 N=12이므로, 다음과 같이 계산하면 54개입니다.
(12-3) * 12 * 0.5 = 54
공식이 생각이 안나요 ㅠㅠ
공식이 있었던 것 같은데, 생각이 안난다면 지금 살펴본 것과 같이 사각형, 오각형과 같이 쉬운 다각형으로부터 공식을 유추해보고 문제를 풀 수 있습니다.
너무 공식을 외우려고 애쓰지 않아도 됩니다. 다만, 외우고 있다면 훨씬 빨리 해결할 수는 있습니다.
[추가] 다각형 내각의 합 구하는 공식?? 이해하면 안외워도되요 https://lucia.tistory.com/34
다각형 내각의 합, 퍼즐 체험으로 이해하기
중등 수학에서 다각형의 내각의 합을 구하고, 또 정다각형일 경우, 한 내각의 크기를 구하는 내용을 다룹니다. 원리에 대한 이해 없이, 외우려고 하면 어려워지는 기하파트입니다. 초등 4학년~5
lucia.tistory.com
[추가] 회전체 어렵지 않아요. https://lucia.tistory.com/125
[활동지 PDF포함] 회전체 알아보기 : 빙글 돌리면 어떤 입체가 만들어질까?
회전체 알아보기 회전체는 평면도형을 회전시켜 만든 입체도형을 말합니다. 정확하게는 평면도형을 한 직선을 축으로 하여 1회전 시킬 때 생기는 입체도형입니다. 원기둥은 직사각형의 한 변을
lucia.tistory.com
.
'아이랑 노는척 공부' 카테고리의 다른 글
| 자와 콤파스로 삼각기둥 전개도 직접 그려서 접어보기 (0) | 2023.01.13 |
|---|---|
| 삼각기둥 전개도가 궁금해? 여러가지 삼각기둥 전개도 알아보기 (0) | 2023.01.13 |
| 여러가지 모양의 사각기둥, 전개도는 어떻게 달라질까? (0) | 2023.01.12 |
| [수학] 정다각형과 각기둥 : 꼭지점, 모서리, 면의 갯수 (전개도PDF 포함) (0) | 2022.12.25 |
| [수학] 원뿔의 높이가 달라지면 전개도가 어떻게 달라지나요? (원뿔전개도PDF파일) (0) | 2022.12.24 |




